A g -spektrumok kiértékelése




A g -spektrumok feldolgozása kizárólag számítógépes programokkal történik, és magába foglalja
 

    A g -spektrum matematikailag egy vektornak tekinthetõ, amelynek elemei (csatornaszámok és beütésszámok) nemnegatív egész számok. A teljesenergia-csúcsok kiválogatása a spektrum többi alkotórészei és a statisztikus ingadozások közül leggyakrabban digitális szûrési és simítási eljárásokkal történik. Közülük legismertebbek a második differenciálhányadost számoló szûrési algoritmusok (pl. a négyszögfüggvény vagy Gauss-görbe második deriváltja), amelyeket a csúcsszélességgel összemérhetõ spektrumrészletre alkalmazunk. A félértékszélesség kalibrációjának ismerete alapvetõ fontosságú a csúcskeresés során. A megfelelõen tág, kiválogatott részekhez (region of interest, ROI) függvényt illesztünk, ami általában összetett és empirikus tagokat is tartalmaz. Az illesztõfüggvény alapvetõen Gauss-görbe. Ezen túlmenõen tartalmazhat például egy gyorslefutású exponenciálist (tökéletlen töltéshordozó összegyûjtés miatt), egy lassú lefutású exponenciálist (a detektorban lejátszódó felületi és szórási jelenségek leírására, a csúcshoz rendelt háttér), lépcsõugrást Gauss-görbével konvolválva (az elsõdleges töltött részecskének a detektor aktív térfogatából történõ kiszökése miatt), mindet a csúcs kisenergiás oldalán, illetve elsõ- vagy másodfokú polinomot a háttér lassan változó részének a leírására. A változók kezdeti értékeit a csúcskeresés által megtalált teljesenergia-csúcsok helyzete, szélességük és más, a ROI-ban meghatározható változók alkotják. Az illesztés bonyolult optimalizációs eljárásokkal történik, gyakran használjuk a súlyozott, nemlineáris legkisebb négyzetek módszerét (nonlinear weighted least squares method) vagy a maximum likelyhood módszert a beütésszámoktól függõen. Az illesztés egyszerre számolja az összes illesztési paramétert, például a csúcsamplitúdót (ami ebben az eljárásban ekvivalens a területtel), a csúcsszélességet, a csúcspozíciót (a maximum vagy centroid, illetve a súlypont helyzetét), az exponenciálisok és a polinom paramétereit. A számításokat az illesztés jóságának a meghatározása is kíséri. Bizonyos feltételek mellett a mért adatok és az illesztési függvény különbségében, maradékában (residuum) újabb csúcskeresés indul meg másfajta csúcskeresõ algoritmussal az összetett csúcsok (multiplettek) felismerésére és kezelésére. Ha a maradékban teljesenergia-csúcs vagy -csúcsok mutatkoznak, akkor többszörös függvénycsoportok illesztése történik. Végezetül a teljesenergia-csúcsok területét számoljuk ki egzakt módon az illesztett paraméterek felhasználásával. A számításokat természetesen intenzív hibaszámítás is kíséri.
    A g -spektrumoknak tehát csak a teljesenergia-csúcsokat tartalmazó részeit értékeljük ki, ellentétben például a röntgen-spektrumokmal, amelynek az egészét szokták illeszteni. Az ismertebb g -spektrum kiértékelõ programok (Hypermet-PC, Sampo-90, Genie-2000, GammaVision-32) általában más, nagyon hasznos részeket, rutinokat (pl. minõségbiztosítást, nuklid azonosítást, minimálisan kimutatható radioaktivitás becslését vagy kalibrációs eljárásokat) is magukba foglalnak.
    Gyors döntésekhez vagy mérés alatt hasznos lehet különálló és nagy csúcsok területének egyszerû számítása, monitorozása. Ha egy csúcs jól megválasztott végpontjai közötti távolság n csatorna és a két végpontok után közvetlenül következõ csatornában a beütésszám rendre B1 és B2, akkor a csúcsalatti A terület trapéz-módszerû háttérlevonással kapható:

A = P – B2·n – (B1 – B2 ) ·n / 2 = P – n / 2 ·(B1 + B2 ) ,

ahol P az adott, n számú csatornák tartalmának az összege.
 
 
A csúcsterület bizonytalansága lényeges csökken, ha a hátteret nem 1, hanem néhány (pl. 3 vagy 5) csatornában mért beütésszám átlagából számoljuk.

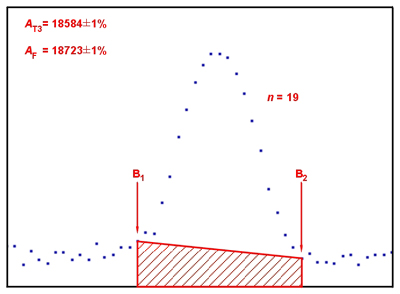
Egy teljesenergia-csúcs területének meghatározása trapéz-módszerel (AT3)
(AF: illesztéssel kapott csúcsterület)

A terület standard deviációja

s A = Ö  (P + n / 2 ·(B1 + B2 ))

.